求陰影部分面積是小學數學中很常見的知識，也是一部分學生覺得比較困難的題型。但只要我們掌握了方法，勤加練習，就能把這些題做出來啦。下面舉幾個例子給大家看一下。

割補法和分割法用于幾何題之中。割補法就是把圖形切開，把切下來的那部分移動到其他位置，使題目便于解答；分割法就是同樣把圖形切開，但是并不移動，使題目便于解答。

首先，第一道題：已知正方形OCDE的邊長，就可以知道扇形的半徑，我們可以用矩形ACDF的面積加上BDE的面積，其中矩形長邊CD=1、短邊AC=O<愛尬聊_百科知識大全>A-OC；然后BDE面積就等于扇形面積減去正方形面積的一半。

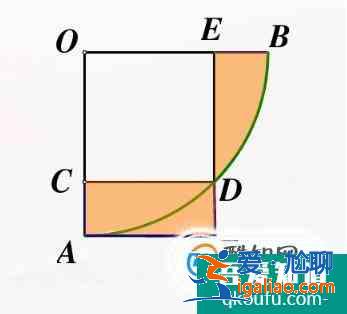
第二道題，我們可以把上面扇形陰影部分補到下面空白處，那么總的陰影面積剛好就是三角形ACD的面積，又因為角ADC是直角，所以陰影部分面積很快就能算出來。

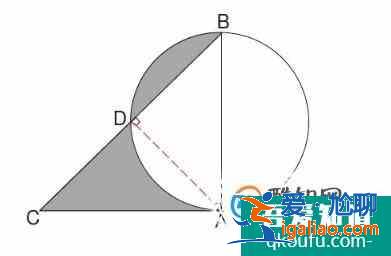
這道題，我們可以用三角形的面積減去三個扇形的面積，三角形是一個正三角形，所以每個扇形的角度都是60°，三個扇形加起來就是半個圓的面積，也很好計算。

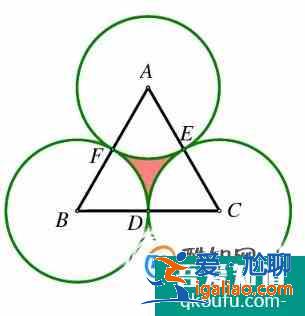
這道題的陰影部分是三個未知角度的扇形，但是三個扇形的半徑都是一樣的，由于三角形的內角和為180°，所以陰影面積就是以扇形半徑為半徑的一個半圓的面積。

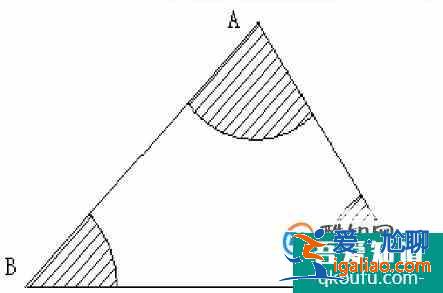
這道題陰影部分是由一個扇形和一個不規則圖形組成，把右上角的扇形割補到左邊相應的空白出，陰影就成了一個三角形，已知三角形的邊長，陰影的面積就可以計算了。