首先，有正弦余弦的和差公式的函數需要記住。記憶方法：觀察這兩個公式，分別叫正弦和余弦，正弦可以聯想到正義，那么余弦就可以聯想到小人了。君子可以不同的在一起合作（正弦的公式里面包含sin和cos）而且表里如一（正負號）；小人一般是跟自己一樣的人在一起（cos在一起，sin在一起），而且喜歡把自己人放在前面（cos在前），表里不如一（正負號）。

以上，你就記住了

接下來記

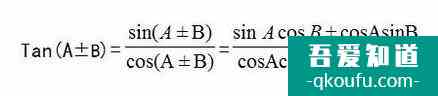
平方關系也得牢記。

式子的右邊同時除以：sinAcosB將式子的右邊同時化為正切的形式，得到：

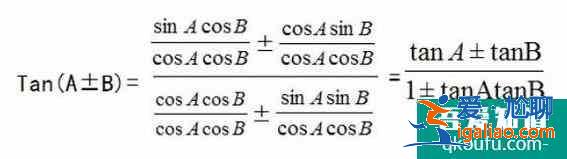
三角形的和差公式：

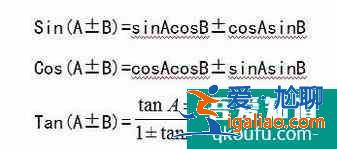
對已經得到的三個公式取正號：

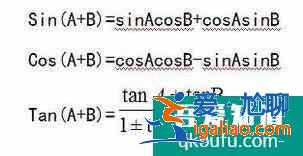
命： A=B得到3個二倍角公式：

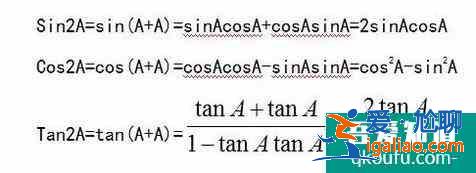
根據

可以對 cos2進行拓展，得到：

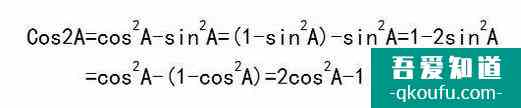
以上二倍角公式：

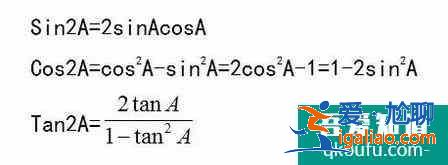
同時：

同時除以

可以得到

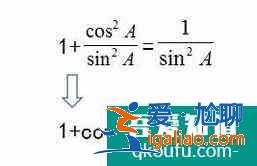
同時除以

總結3個平方公式：

由二倍角公式

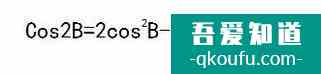
令 A=2B，得到：

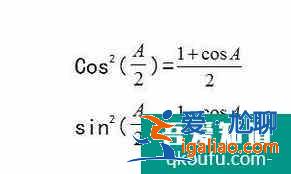
也就是半角公式：

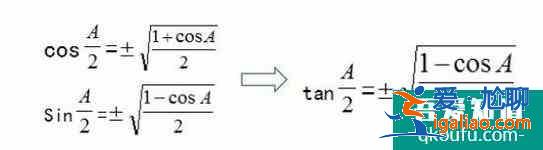
其中正負看A的范圍。

根據三角形的正弦和差公式求積化和差公式：

正負號兩式相加：2sinCcosD=sin(C+D)+sin(C-D)兩式相減：2cosCsinD=sin(C+D)-sin(C-D)(實際和上面是統一個公式）根據三角形的余弦和差公式

正負號兩式相加：2sinCcosD=sin(C+D)+sin(C-D)兩式相減：2sinCsinD=cos(C-D)-cos(C+D)和差化積公式：2sinCcosD=sin(C+D)+sin(C-D)2cosCcosd=cos(C+D)+cos(C-D)2sinCsinD=cos(C-D)-cos(C+D)令: C+D=A；<愛尬聊_百科詞條>C-D=B得到

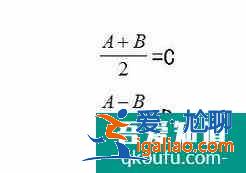
可得到積化和差公式：

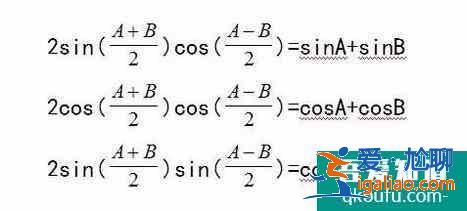
萬能公式：由二倍角公式

令： 2B=A得到

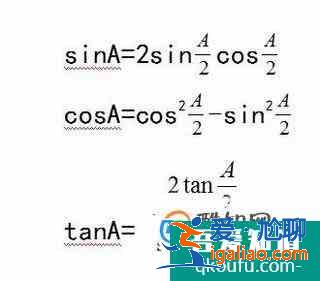
對第一和第二個公式分別除以1，也就是

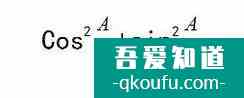
得到

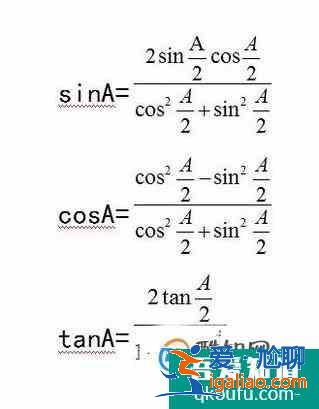
兩式右面分貝除以

得到

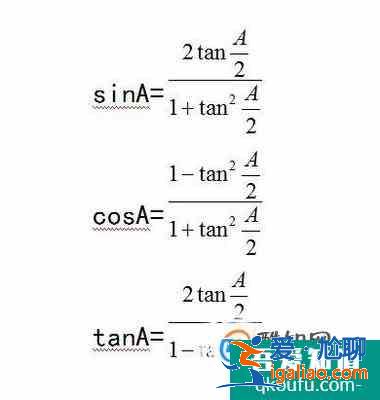
將

帶入三角形的和差公式可得到各類誘導公式，當然你也可以用“奇變偶不變，符號看象限”來記憶。