線性代數:如何求特征值和特征向量??
線性代數的學習中,掌握方法很重要。下面就為大家慢慢解析,如何求特征值和特征向量。
特征值和特征向量的相關定義01首先我們需要了解特征值和特征向量的定義,如下圖;

齊次性線性方程組和非其齊次線性方程組的區別,如下圖;
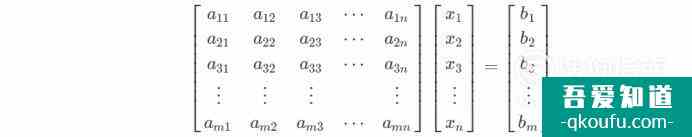
特征子空間的定義,如下圖;


特征多項式的定義,如下圖;

特征值的基本性質,如下圖;

齊次線性方程組的特征就是等式右邊為0,以消元法簡化;

在初等數學方程組中都是有唯一解的,而在線性代數中,我們把這種情況稱為方程組“系數矩陣的秩為1”,記為r(A)=1,當矩陣的秩小于未知數的個數時,方程組有無數個解;當矩陣的秩等于未知數的個數時,方程組只有零解。由于上訴方程組有兩個未知數,而r(A)=1<2,所以此組有無數個解。設 y=2 ,則 x=1;再設k為任意常數,則 x=k, y=2k為方程組的解,寫成矩陣的形式為:

非齊次線性方程組因為不等于0,看起來很復雜,其實方法還是先用消元法簡化步驟;

這一次進行初等行變換后,對于任意的非齊次線性方程組,當 r(A)=r(A|b)=未知數的個數時,非齊次線性方程組有唯一解;當 r(A)=r(A|b)<未知數的個數時,非齊次線性方程組有無數個解;當 r(A) ≠r(A|b) 時,非齊次線性方程組無解。可見 r(A)=r(A|b)=3,所以[A|b]有唯一解,寫回方程組形式:

求下列矩陣的特征值和特征向量;

求矩陣特征值和特征向量的一般解法;
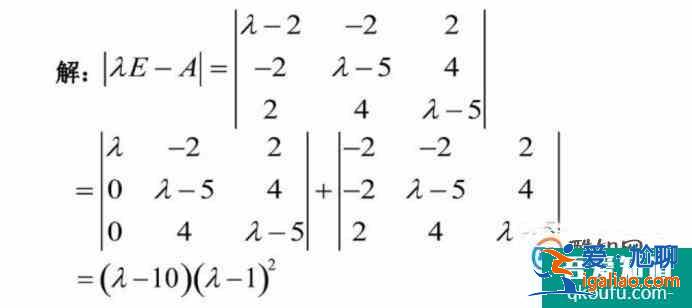

試證明A的特征值唯有1和2;
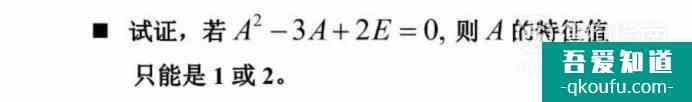
證明性問題還是需<愛尬聊_尬聊生活>要解出特征值。
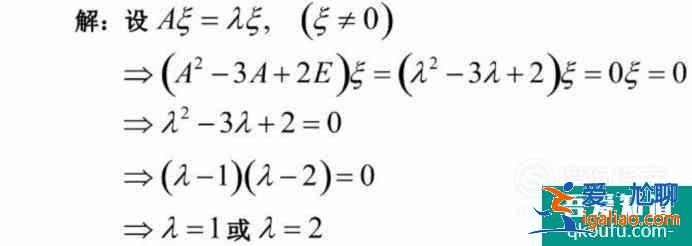
對于特征值與特征向量,總結起來大概分為三種理解:

